Viscosidad sanguínea y perfiles de flujo. Continuidad. Ley de POISEVILLE.

Un fluido se desplaza en el interior de un tubo cuando la presión en el inicio es superior a la existente al final del tubo, moviéndose desde una zona de mayor presión a una de menor presión. El flujo o caudal depende directamente del gradiente o diferencia de presión entre esos dos puntos e inversamente de la resistencia, en una relación similar a la de Ohm para los circuitos eléctricos.

La resistencia depende de las dimensiones del tubo y de la naturaleza del fluido, y mide las fuerzas de rozamiento o fricción entre las propias moléculas del fluido y entre éstas y las moléculas de la pared del tubo. La velocidad con la que circula la sangre en el interior de un tubo es directamente proporcional al flujo e inversamente proporcional al área transversal del tubo.

Q (flujo o caudal) = ΔP (P1 – P2) / R (resistencia)

El flujo o caudal (volumen/minuto) se define también como el volumen circulante por un segmento transversal del circuito en la unidad de tiempo:

Tipos de flujo.

·         Flujo laminar

En condiciones fisiológicas el tipo de flujo mayoritario es el denominado flujo en capas o laminar. El fluido se desplaza en láminas coaxiales o cilíndricas en las que todas las partículas se mueven sin excepción paralelamente al eje vascular. Se origina un perfil parabólico de velocidades con un valor máximo en el eje o centro geométrico del tubo.

En el caso del sistema vascular los elementos celulares que se encuentran en sangre son desplazados tanto más fuertemente hacia el centro cuanto mayor sea su tamaño.

·        Flujo turbulento

En determinadas condiciones el flujo puede presentar remolinos, se dice que es turbulento. En esta forma de flujo el perfil de velocidades se aplana y la relación lineal entre el gradiente de presión y el flujo se pierde porque debido a los remolinos se pierde presión.

Para determinar si el flujo es laminar o turbulento se utiliza el número de Reynolds (NR), un número adimensional que depende de:

r, radio (m) velocidad media (m/s), densidad (g/cc) y la viscosidad (Pa.s).

En la circulación sanguínea en regiones con curvaturas pronunciadas, en regiones estrechadas o en bifurcaciones, con valores por encima de 400, aparecen remolinos locales en las capas limítrofes de la corriente. Cuando se llega a 2000-2400 el flujo es totalmente turbulento. Aunque la aparición de turbulencias no es deseable por el riesgo que tienen de producir coágulos sanguíneos, se pueden utilizar como procedimientos diagnósticos, ya que mientras el flujo laminar es silencioso, el turbulento genera ruidos audibles a través de un estetoscopio.

Resistencias vasculares

La resistencia no puede medirse directamente por ser una magnitud compuesta, pudiendo obtenerse de la ecuación inicial al establecer un gradiente de presión entre dos puntos y medir el flujo que se establece:

 (mmHg. min/ml, URP → unidad de resistencia periférica hemodinámica).

Su magnitud depende de las dimensiones del tubo por donde circula el fluido, de su viscosidad y del tipo de flujo o corriente que se realice.

Tipos de resistencia

La resistencia periférica total es la suma de las resistencias vasculares. Los vasos sanguíneos en el sistema vascular constituyen una red en la que determinados segmentos se sitúan en serie y otros en paralelo. La resistencia varía dependiendo de la colocación de los vasos.

Viscosidad

Uno de los factores que determina la resistencia al movimiento de los fluidos son las fuerzas de rozamiento entre las partes contiguas del fluido, las fuerzas de viscosidad.

La viscosidad (η) se define como la propiedad de los fluidos, principalmente de los líquidos, de oponer resistencia al desplazamiento tangencial de capas de moléculas. Según Newton, resulta del cociente entre la tensión de propulsión (τ) o fuerza de cizalladura y el gradiente de velocidad (Δν) entre las distintas capas de líquidos.

Las unidades de η son Pascales/seg. Los fluidos newtonianos u homogéneos son los que muestran una viscosidad constante, como el agua, o las soluciones de electrolitos; por el contrario, los fluidos no newtonianos, o heterogéneos, presentan una viscosidad variable, es el caso de la sangre que se modifica dependiendo de las dimensiones del tubo y del tipo de flujo. Cuando la velocidad de la sangre se incrementa la viscosidad disminuye.

La ley de Poiseuille

También conocida como ley de Hagen-Poiseuille, después de los experimentos llevados a cabo en 1839 por Gotthilf Heinrich Ludwig Hagen es una ley que permite determinar el flujo laminar estacionario ΦV de un líquido incompresible y uniformemente viscoso (también denominado fluido newtoniano) a través de un tubo cilíndrico de sección circular constante. Esta ecuación fue derivada experimentalmente en 1838, formulada y publicada en 1840 y 1846 por Jean Louis Marie Poiseuille (1797-1869). La ley queda formulada del siguiente modo:

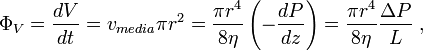
Donde V es el volumen del líquido que circula en la unidad de tiempo t, vmedia la velocidad media del fluido a lo largo del eje z del sistema de coordenadas cilíndrico, r es el radio interno del tubo, ΔP es la caída de presión entre los dos extremos, η es la viscosidad dinámica y L la longitud característica a lo largo del eje z. La ley se puede derivar de la ecuación de Darcy-Weisbach, desarrollada en el campo de la hidráulica y que por lo demás es válida para todos los tipos de flujo. La ley de Hagen-Poiseuille se puede expresar también del siguiente modo:

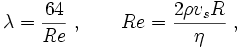
Donde Re es el número de Reynolds y ρ es la densidad del fluido. En esta forma la ley aproxima el valor del factor de fricción, la energía disipada por la pérdida de carga'RTYERY', el factor de pérdida por fricción o el factor de fricción de Darcy λ en flujo laminar a muy bajas velocidades en un tubo cilíndrico. La derivación teórica de la fórmula original de Poiseuille fue realizada independientemente por Wiedman en 1856 y Neumann y E. Hagenbach en 1858 (1859, 1860). Hagenbach fue el primero que la denominó como ley de Poiseuille.

La ley es también muy importante en hemodinámica.

La ley de Poiseuille fue extendida en 1891 para flujo turbulento por L. R. Wilberforce, basándose en el trabajo de Hagenbach.